Quantum-enhanced Markov chain Monte Carlo optimisation
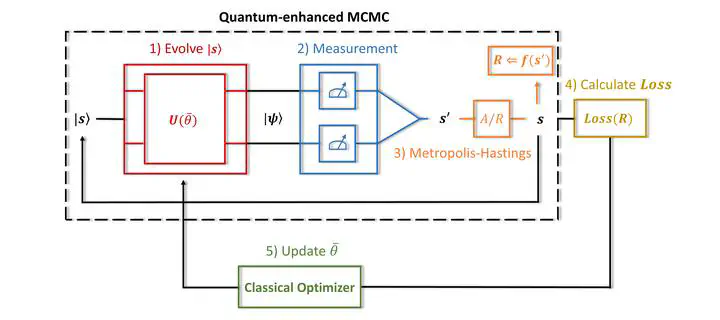 High-level representation of the optimisation algorithm.
High-level representation of the optimisation algorithm.Currently, I am in the process of finalizing and preparing this project for submission to a peer‑reviewed journal.
The combination of classical Markov chains Monte Carlo (MCMC) methods with quantum computers showed potential for achieving quantum advantage in sampling from the Boltzmann probability distribution, a computationally hard task arising in many diverse fields. Quantum-enhanced proposal distributions, defined by parameterized unitaries, could outperform classical strategies in proposing effective MCMC moves. However, it is crucial to carefully tune the values of the parameters defining the quantum proposal distribution, as they determine the resulting advantage over the classical counterpart. A general optimization method becomes essential when considering parameterized unitaries for which is not possible to identify a reasonable parameter set. This could happen when adopting complicated proposal strategies depending on a large number of parameters, or simply when no prior or relevant information is available. In the present work, we propose a general optimisation algorithm that exploits estimates of the autocorrelation function of a certain observable, calculated over a set of samples, to optimise the parameters defining the proposal distributions.
A Python simulator of the first version of the algorithm is available on my GitHub.
Read the full thesis here.